Formeln am Sanjiegun-Viereck
Auf dieser Seite werden ausgewählte Berechnungen am Viereck mit drei gleichen Seiten ausgeführt, welches ich nach einer traditionellen chinesischen Waffe Sanjiegun hier Sanjiegun-Viereck nennen möchte. Am Ende werden die Ergebnisse auf Spiegeldreiecke angewendet.
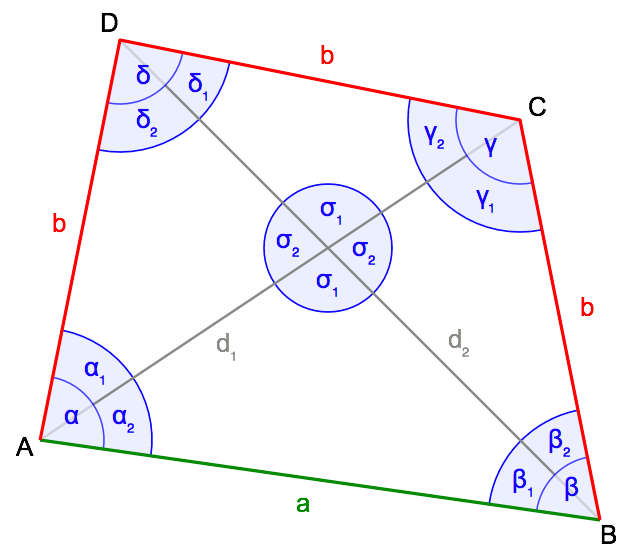
Wie es in Abbildung 1 dargestellt ist, sind in diesem Artikel die Ecken des Sanjiegun-Vierecks im Uhrzeigersinn mit A, B, C, D benannt. In ihnen liegen die Winkel α, β, γ, δ, welche jeweils durch die Diagonalen in α₁, α₂; β₁, β₂ et cetera geteilt werden. Die Seite AB weist die Länge a, die drei gleichen Seiten BC, CD und DA die Länge b auf. Die Winkel zwischen den sich in S schneidenden Diagonalen AC der Länge d₁ und BD der Länge d₂ heißen σ₁ und σ₂, wobei σ₁ der Seite AB gegenüberliegt.
Schnittwinkel der Diagonalen
Satz 1: In einem Sanjiegun-Viereck entspricht die halbe Summe der von den gleichen Seiten eingeschlossenen Winkel dem der vierten Seite gegenüberliegenden Schnittwinkel der Diagonalen. Mit den Bezeichnungen aus Abbildung 1 heißt das: $\sigma_1=\frac{\gamma+\delta}{2}$.
Satz 2: Der Nebenwinkel jenes Schnittwinkels entspricht der halben Summe der an der vierten Seite anliegenden Winkel, also: $\sigma_2=\frac{\alpha+\beta}{2}$.
Beweis
Da die Dreiecke ACD und BCD gleichschenklig sind, lassen sich ihre Basiswinkel mithilfe der Innenwinkelsumme im Dreieck zu $\alpha_1=\gamma_2=\frac{\pi-\delta}{2}$ und $\beta_2=\delta_1=\frac{\pi-\gamma}{2}$ berechnen. Wieder mit der Innenwinkelsumme im Dreieck, hier das Dreieck CDS, gilt
Für die Innenwinkelsumme im Viereck gilt $\alpha+\beta+\gamma+\delta=2\pi$, für die Schnittwinkel $2\pi=2\sigma_1+2\sigma_2$. Setzt man diese Formeln gleich und das obige Ergebnis ein …
… erhält man durch Umstellen der Gleichung das Ergebnis: $\sigma_2=\frac{\alpha+\beta}{2}$.
Längen der Diagonalen
Satz 3: In einem Sanjiegun-Viereck messen die Diagonalen das doppelte Produkt der mehrfach vorkommenden Seitenlänge mit dem Sinus des halben, der Diagonalen gegenüberliegenden, von gleichen Seiten eingeschlossenen Winkels. Mit den Bezeichnungen aus Abbildung 1 gelten also $d_1=2b\sin\frac{\delta}{2}$ und $d_2=2b\sin\frac{\gamma}{2}$.
Beweis
Zunächst gilt mit dem Kosinussatz im Dreieck ACD:
Zieht man nun beiderseits die Wurzel und greift dann auf die geeignete Halbwinkelformel zurück, erhält man:
Der Beweis für $d_2=2b\sin\frac{\gamma}{2}$ erfolgt analog.
Seitenbeziehung mit eingeschlossenen Winkeln
Satz 4: Der Quotient aus Seitenlänge a und der im Sanjiegun-Viereck dreimal vorkommenden Seitenlänge b lässt sich in Abhängigkeit von den durch die drei gleichen Seiten eingeschlossenen Winkel γ und δ folgendermaßen darstellen:
Satz 5: Die folgende Darstellung ist dazu äquivalent:
Beweis zu Satz 4
Mit dem Kosinussatz und den obigen Ausführungen gilt im Dreieck ABC:
In einem ersten Schritt der Umformung werden beide Seiten der Gleichung durch $b^2$ geteilt und ausgenutzt, dass sich die Kosinusfunktion durch eine phasenverschobene Sinusfunktion darstellen lässt:
Mit dem geeigneten Additionstheorem wird daraus:
Ausmultiplizieren und Ausklammern bringt nun:
Anwenden der Formeln zu Halb- bzw. Doppelwinkelfunktionen führt zu folgender Darstellung, in der nun klar ersichtlich ist, dass sich der Quotient der Seitenlängen a und b bei einem Vertauschen der Winkel γ und δ nicht ändert:
Das Auflösen der Klammern durch Ausmultiplizieren erbringt:
Eine erneute Anwendung der Additionstheoreme resultiert in:
Zieht man auf beiden Seiten der Gleichung die Quadratwurzel, erhält man die behauptete Beziehung:
Beweis zu Satz 5
Steigen wir noch einmal an dieser Stelle des Beweises zu Satz 4 ein:
Durch Anwenden der Halb- bzw. Doppelwinkelfunktionen lässt sich dies auch umwandeln in diese Darstellung:
Ausklammern erbringt:
Ausnutzen des geeigneten Additionstheorems führt nun hierher:
Dank den Symmetrien der Kosinusfunktion lässt sich dies umwandeln zu:
Beiderseitiges Ziehen der Wurzel bringt dann die gesuchte Darstellung:
Anwendung: Spiegeldreiecke
Sanjiegun-Vierecke spielen nicht nur bei der Auseinandersetzung mit traditionellen chinesischen Waffen eine Rolle. Sie tauchen zum Beispiel bei der Konstruktion von Spiegeldreiecken auf, wie Abbildung 2 zeigt.
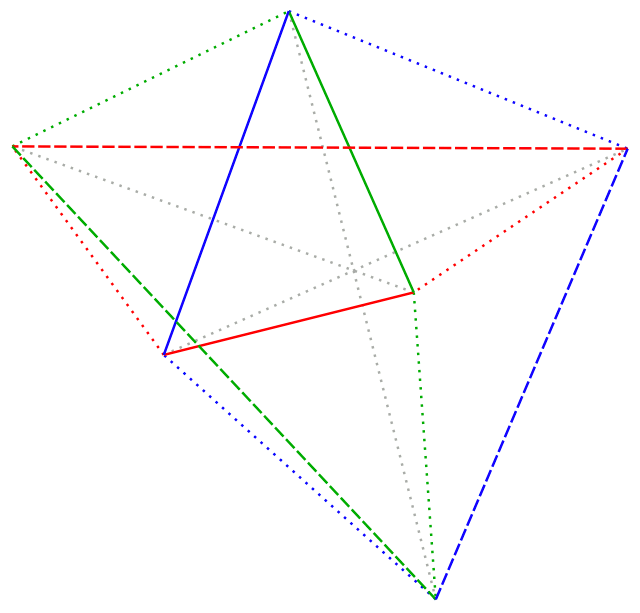
Betrachten wir ein Dreieck mit den Winkeln κ, λ, μ und den diesen Winkeln gegenüberliegenden Seiten der Längen k, l und m. Die Seitenlängen dessen Spiegeldreiecks sollen K, L und M heißen, sodass K mit dreimal k, L mit dreimal l und M mit dreimal m Sanjiegun-Vierecke bilden. Satz 5 gibt nun fürs Verhältnis der Seiten des Ausgangs- und des Spiegeldreiecks folgende elegante Resultate: