Spiegeldreieck eines Dreiecks

Spiegelt man die Punkte eines Dreiecks an der jeweils gegenüberliegenden Seite des Dreiecks, erhält man drei neue Punkte. Das neue Dreieck, welches diese Punkte bilden, wird Spiegeldreieck1 des ersten Dreiecks genannt.

Abbildung 1: Ein Spiegeldreieck entsteht, wenn ein Dreieck (rot) an seinen eigenen Seiten gespiegelt wird (grün) und die durch diesen Vorgang neu entstandenen Punkte miteinander verbunden werden (blau). Eingezeichnet sind auch die verlängerten Höhen (grau) des Ausgangsdreiecks.

Auf dieser Seite werden grundlegende Eigenschaften des Spiegeldreiecks dargestellt. Zunächst allerdings eine Übersicht über Voraussetzungen für die folgenden Betrachtungen.

Voraussetzungen

Dreieck

Ein Dreieck ist durch drei Punkte, die nicht alle auf einer Geraden liegen, definiert. Hier werden sie $A, B, C$ genannt. Die Länge der Seite $\overline{BC}$ wird a, die Länge der Seite $\overline{AC}$ wird b und die Länge der Seite $\overline{AB}$ wird c genannt. Die Winkel an den Eckpunkten $A, B, C$ heißen in dieser Reihenfolge $\alpha, \beta, \gamma$.

Beziehung der Seitenlängen

Zwei Seiten eines Dreiecks sind zusammen stets länger als die dritte Seite:

$$\begin{aligned} a+b-c &> 0 \\ a+c-b &> 0 \\ b+c-a &> 0 \end{aligned}$$

Kosinussatz

Der Kosinussatz2 setzt die Seitenlängen eines Dreiecks $a, b, c$ in Beziehung zum Kosinus eines Winkels:

$$\begin{aligned} a^2 &= b^2+c^2-2bc\cos\alpha \\ b^2 &= a^2+c^2-2ac\cos\beta \\ c^2 &= a^2+b^2-2ab\cos\gamma \end{aligned}$$

Umgestellt nach dem Kosinus des Winkels gilt also auch:

$$\begin{aligned} \cos\alpha &= \frac{b^2+c^2-a^2}{2bc} \\ \cos\beta &= \frac{a^2+c^2-b^2}{2ac} \\ \cos\gamma &= \frac{a^2+b^2-c^2}{2ab} \end{aligned}$$

Kosinusprodukt

Mit dem Kosinussatz ist das Produkt der Kosinus aller Winkel:

$$\begin{aligned} \cos\alpha\,\cos\beta\,\cos\gamma &= \frac{(a^2+b^2-c^2)(a^2+c^2-b^2)(b^2+c^2-a^2)}{8a^2b^2c^2} \\ &= \frac{b^2c^4+a^2c^4+b^4c^2+a^4c^2+a^2b^4+a^4b^2-2a^2b^2c^2-a^6-b^6-c^6}{8a^2b^2c^2} \end{aligned}$$

Winkeldreifaches

Der Kosinus des Winkeldreifachen lässt sich wie folgt auflösen:2

$$\cos(3\alpha) = 4(\cos\alpha)^3-3\cos\alpha$$

Dreiecksfläche

Die Dreiecksfläche, hier als $\Delta$ bezeichnet, berechnet sich als:2

$$\Delta = \frac{1}{4}\sqrt{(b+c-a)(a+b-c)(a+c-b)(a+b+c)}$$

Demnach ist:

$$16\Delta^2 = (b+c-a)(a+b-c)(a+c-b)(a+b+c)$$

Seitenlängen des Spiegeldreiecks

Abbildung 2: Dreieck und Spiegeldreieck mit Beschriftung einer Auswahl von Seitenlängen und Winkeln.

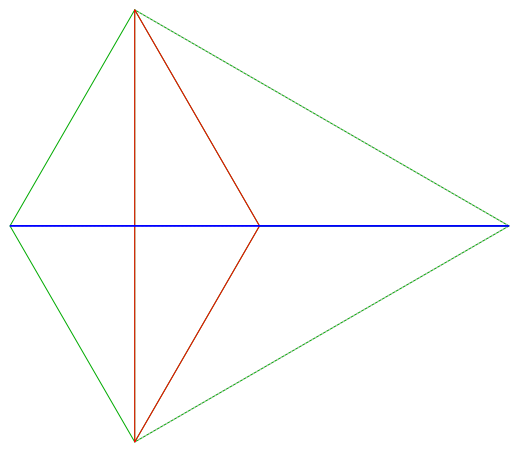
Abbildung 2 zeigt, dass die Seitenlängen $a_s, b, c$ ein Hilfsdreieck bilden, in welchem der $a_s$ gegenüberliegende Winkel $3\alpha$ entspricht. Nach dem Kosinussatz gilt für das Quadrat über der Seitenlänge $a_s$ des Spiegeldreiecks also:

$${a_s}^2 = b^2+c^2-2bc\cos(3\alpha)$$

Das Winkeldreifache aufgelöst, wird daraus:

$${a_s}^2 = b^2+c^2-2bc\left(4(\cos\alpha)^3-3\cos\alpha\right)$$

Erneute Anwendung des Kosinussatzes ergibt:

$$\begin{aligned} {a_s}^2 &= b^2+c^2-2bc\left(4\left(\frac{b^2+c^2-a^2}{2bc}\right)^3-3\left(\frac{b^2+c^2-a^2}{2bc}\right)\right) \\ &= 4b^2+4c^2-3a^2-\frac{\left(b^2+c^2-a^2\right)^3}{b^2c^2} \end{aligned}$$

Weiteres Umstellen ergibt:

$${a_s}^2 = a^2+\frac{(b+c-a)(a+c-b)(a+b-c)(a+b+c)(b^2+c^2-a^2)}{b^2c^2}$$

Mit der Dreiecksfläche und dem Kosinussatz lässt sich dies kürzer ausdrücken als:

$${a_s}^2 = a^2+\frac{32\Delta^2}{bc}\cos\alpha$$

Auch die Seitenlängen $a, b, c_s$ bilden ein Hilfsdreieck, wie in Abbildung 2 gezeigt wird. Der $c_s$ gegenüberliegende Winkel beträgt dort zwar $2\pi-3\gamma$. Da aber mit dem Kosinus des Winkels gearbeitet wurde und $\cos(2\pi-x)=\cos x$ ist, lässt sich die obige Herleitung problemlos auf alle Seiten übertragen:

$$\begin{aligned} {b_s}^2 &= b^2+\frac{(b+c-a)(a+c-b)(a+b-c)(a+b+c)(a^2+c^2-b^2)}{a^2c^2} \\ &= b^2+\frac{32\Delta^2}{ac}\cos\beta \\ {c_s}^2 &= c^2+\frac{(b+c-a)(a+c-b)(a+b-c)(a+b+c)(a^2+b^2-c^2)}{a^2b^2} \\ &= c^2+\frac{32\Delta^2}{ab}\cos\gamma \end{aligned}$$

Gut ersichtlich ist, dass eine beliebige Seitenlänge b eines Dreiecks kleiner als die entsprechende Seitenlänge $b_s$ im Spiegeldreieck ist, wenn es sich beim zugehörigen Winkel β mit $\cos\beta>0$ um einen spitzen Winkel handelt. Im Fall eines rechten Winkels ist $\cos\beta=0$ und die Seiten sind gleich lang. Ist der Winkel stumpf, gilt $\cos\beta<0$ und die ihm gegenüberliegende Seite des Dreiecks ist länger als die entsprechende Seite im Spiegeldreieck.

Abbildung 3: Ein stumpfwinkliges Dreieck (rot) mit seinen Spiegelbildern (grün) und Spiegeldreieck (blau).

Fläche des Spiegeldreiecks

Die Dreiecksfläche $\Delta_s$ des Spiegeldreiecks berechnet sich wie folgt:

$$\begin{aligned} \Delta_s &= \frac{1}{4}\sqrt{(a_s+b_s-c_s)(a_s+c_s-b_s)(b_s+c_s-a_s)(a_s+b_s+c_s)} \\ &= \frac{1}{4}\sqrt{{a_s}^4+{b_s}^4+{c_s}^4-\left({a_s}^2-{b_s}^2\right)^2-\left({a_s}^2-{c_s}^2\right)^2-\left({b_s}^2-{c_s}^2\right)^2} \end{aligned}$$

Darin können die Seitenlängen-Formeln eingesetzt werden. Ausgeklammert ergibt das dann:

$$\Delta_s = \frac{1}{4}\sqrt{\frac{(a+b-c)(a+c-b)(b+c-a)(c+b+a)(b^2c^4+a^2c^4+b^4c^2+a^4c^2+a^2b^4+a^4b^2+a^2b^2c^2-a^6-b^6-c^6)^2}{a^4b^4c^4}}$$

Anwenden der Formel zur Dreiecksfläche und Ziehen der Wurzel resultiert in:

$$\Delta_s = \Delta\cdot\left|\frac{b^2c^4+a^2c^4+b^4c^2+a^4c^2+a^2b^4+a^4b^2+a^2b^2c^2-a^6-b^6-c^6}{a^2b^2c^2}\right|$$

Sehr kurz darstellen lässt sich dies, greift man auf das Kosinusprodukt zurück:

$$\Delta_s = \Delta\cdot|8\cos\alpha\,\cos\beta\,\cos\gamma+3|$$

Diese Formel zeigt nebenbei, dass Dreiecke mit $\cos\alpha\,\cos\beta\,\cos\gamma=-\frac{3}{8}$ kein Spiegeldreieck besitzen. Die Punkte, die sonst das Spiegeldreieck bilden, liegen dann auf einer Geraden.

Abbildung 4: Gleichschenkliges Beispiel für ein Dreieck (rot) ohne Spiegeldreieck. Das Dreieck besitzt Basiswinkel von $\frac{1}{6}\pi=30^{\circ}$ und das Seitenverhältnis $1:1:\sqrt{3}$. Die Spiegelpunkte liegen auf einer Geraden (blau). Hier fallen sogar zwei der drei Spiegelpunkte in einem Punkt zusammen.

In einem Folgeartikel werden das Kosinusprodukt und besondere Eigenschaften der Spiegeldreiecke von spitzwinkligen Dreiecken näher betrachtet.

  1. Freie Übersetzung von reflection triangle auf Wolfram Mathworld. Abgesehen von der Bezeichnung wurden keine Inhalte von jener Seite übernommen.
  2. Wikipedia: Formelsammlung Trigonometrie, Abrufdatum 2011-02-27.