Ein Stück vom Kuchen
oder Schicksal zweier Folgen bei negativer Diskriminante

Stell Dir vor, Du hast einen köstlichen, runden Kuchen vor Dir. Von der Mitte aus zum Rand machst Du zwei Schnitte und teilst den Kuchen damit in zwei ungleiche Teile. Ist es jetzt noch möglich, den ganzen Kuchen in gleich große Stücke zu schneiden – egal wie viele, egal wie schmal, Hauptsache gleich groß?

Es mag auf den ersten Blick erstaunen, aber die Antwort auf diese Frage klärt ebenfalls, ob die in zwei vorangegangenen Artikeln1 betrachteten Folgenscharen bei negativer Diskriminante $\Delta=p^2-4q$ irgendwann abbrechen oder sich unendlich weiter entwickeln.

Dieser Artikel macht sich auf die Suche nach einer Antwort. Zuerst jedoch eine Rückschau auf den positiven Fall, um dann zu betrachten, wo sich beide Szenarien unterscheiden.

Rückblick: positive Diskriminante

In den vorangegangen Artikeln wurden $p,q\in\mathbb{R}\setminus\{0\}$ und $p^2>4q$, also $\Delta>0$, sowie $n\in\mathbb{N}$ vorausgesetzt. Dann galten:

$$\begin{aligned} \alpha(n) &= q\frac{b^{n-1}-a^{n-1}}{b^n-a^n} = \begin{cases} 0 & \mathrm{falls\quad} n=1 \\ -\frac{q}{p+\alpha(n-1)} & \mathrm{falls\quad} n>1 \end{cases} \\ \beta(n) &= \frac{b^{n+1}-a^{n+1}}{b^n-a^n} = \begin{cases} -p & \mathrm{falls\quad} n=1 \\ -p-\frac{q}{\beta(n-1)} & \mathrm{falls\quad} n>1 \end{cases} \end{aligned}$$

Dabei sind a und b die beiden reellwertigen Lösungen der quadratischen Gleichung $0=x^2+px+q$:

$$\begin{aligned} a &= -\frac{p}{2}-\sqrt{\frac{p^2}{4}-q} = -\frac{p+\sqrt{\Delta}}{2} \\ b &= -\frac{p}{2}+\sqrt{\frac{p^2}{4}-q} = -\frac{p-\sqrt{\Delta}}{2} \end{aligned}$$

Auffällig ist zum einen, dass wegen $\Delta>0$ die Lösungen a und b als reelle Zahlen existieren, denn die Quadratwurzel der Diskriminante ist reell definiert.

Zum anderen fällt auf, dass $b^n\neq a^n$ gelten muss, da ansonsten eine Division durch null vorgenommen würde. $b^n$ gleich $a^n$ könnte bei reellen Zahlen auftreten, wäre n gleich 0 und/oder a und b hätten gleiche Beträge. Da aber $n\in\mathbb{N}$ vorausgesetzt wurde, ist $n\neq 0$. Dass $|b|\neq |a|$ ebenfalls aus den Voraussetzungen $p\neq 0$ und $p^2>4q$ folgt, zeigte ich in den Vorbetrachtungen zum Artikel über die Grenzwerte der Folgenscharen α und β.

Andere Lage bei negativer Diskriminante

Ist die Diskriminante negativ, sieht es anders aus. Die quadratische Gleichung besitzt keine reellen Lösungen mehr. a und b sind aber als komplexe Lösungen definiert

$$\begin{aligned} a &= -\frac{p}{2}-\mathrm{i}\sqrt{q-\frac{p^2}{4}} = -\frac{p+\mathrm{i}\sqrt{-\Delta}}{2} \\ b &= -\frac{p}{2}+\mathrm{i}\sqrt{q-\frac{p^2}{4}} = -\frac{p-\mathrm{i}\sqrt{-\Delta}}{2} \end{aligned}$$

wobei $\mathrm{i}$ für die imaginäre Einheit steht. Eine Lösung ist jeweils die komplex Konjugierte der anderen Lösung, also die in der komplexen Zahlenebene an der reellen Achse gespiegelte Zahl:

Abbildung 1: Mit $\Re$ ist die reelle Achse bezeichnet – sie entspricht der vertrauten Zahlengerade aus Schulzeiten. $\Im$ bezeichnet die imaginäre Achse – auf ihr wird die zweite Komponente einer komplexen Zahl $z=\Re(z)+\mathrm{i}\Im(z)$ aufgetragen. Beide Achsen spannen die komplexe Zahlenebene auf.

Komplexer Betrag

Auch für komplexe Zahlen ist ein Betrag definiert. Der Betrag einer Zahl z entspricht dem Abstand zwischen z und dem Ursprung 0 in der komplexen Zahlenebene. So lässt sich der Betrag mit dem Satz des Pythagoras berechnen:

$$|z| = \left|\Re(z)+\mathrm{i}\Im(z)\right| = \sqrt{\left(\Re(z)\right)^2+\left(\Im(z)\right)^2}$$

Konjugierte Zahlen besitzen stets gleiche Beträge. Auf a und b angewendet:

$$\begin{aligned} |a| = \left|\left(-\frac{p}{2}\right)+\mathrm{i}\left(-\sqrt{q-\frac{p^2}{4}}\right)\right| &= \sqrt{\left(-\frac{p}{2}\right)^2+\left(-\sqrt{q-\frac{p^2}{2}}\right)^2} = \sqrt{q} \\ |b| = \left|\left(-\frac{p}{2}\right)+\mathrm{i}\left(\sqrt{q-\frac{p^2}{4}}\right)\right| &= \sqrt{\left(-\frac{p}{2}\right)^2+\left(\sqrt{q-\frac{p^2}{2}}\right)^2} = \sqrt{q} \end{aligned}$$

Für $\Delta<0$ gilt also immer $|a|=|b|=\sqrt{q}$. Bedeutet dies, dass bei negativer Diskriminante die Folgen unweigerlich eine Division durch null verursachen? Nein! Denn für komplexe Zahlen folgt aus $|a|=|b|$ noch nicht, dass Potenzen von a und b mit natürlichem Exponenten gleich werden. Damit dies passiert, müssen die Beträge gleich sein, aber es reicht nicht aus, dass sie gleich sind.

Komplexes Argument

Argument $\arg(z)$ einer komplexen Zahl z nennt man den Winkel zwischen der positiven reellen Achse und dem im Ursprung beginnenden Strahl durch die komplexe Zahl. Berechnen lässt sich der Winkel über die Arkusfunktionen, z. B. den Arkuskosinus:

$$\arg(z) = \begin{cases} +\arccos\dfrac{\Re(z)}{|z|} &\mathrm{falls\quad} \Im(z)\geq 0 \\ -\arccos\dfrac{\Re(z)}{|z|} &\mathrm{falls\quad} \Im(z)<0 \end{cases}$$

Für den Winkel $\phi:=\arg(b)$ gilt demnach:

$$\begin{aligned} \phi &= \arccos\frac{\Re(b)}{|b|} \\ &= \arccos\frac{-\frac{p}{2}}{\sqrt{q}} \\ &= \arccos\left(-\frac{p}{2\sqrt{q}}\right) \end{aligned}$$

In der komplexen Zahlenebene:

Abbildung 2: Darstellung von a und b mit Polarkoordinaten. Ihr Radius (Betrag) ist gleich, ihr Winkel (Argument) unterscheidet sich nur durch das Vorzeichen.

Der Winkel „zwischen den Lösungen“, welcher durch die positive reelle Achse halbiert wird, beträgt $2\phi$.

Komplexe Wurzeln

Mit den n-ten Wurzeln einer komplexen Zahl z meint man die n Lösungen der Gleichung $y^n=z$. Diese Lösungen besitzen alle denselben Betrag, sie liegen also auf einem Kreis in der komplexen Zahlenebene, dessen Mittelpunkt die 0 ist. Mehr noch: Die Lösungen teilen den Kreis, auf dem sie liegen, in n gleich große Bögen.

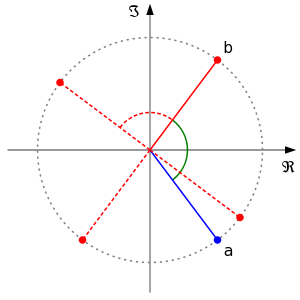
Abbildung 3: Die vier roten Punkte markieren b sowie genau jene drei Zahlen $b_2, b_3, b_4$, für die gilt: $b^4=b_2^4=b_3^4=b_4^4$. In der komplexen Zahlenebene verteilen sich diese Zahlen gleichmäßig auf den Kreis aller Zahlen mit demselben Betrag. Zwar besitzt auch a den gleichen Betrag, wird aber von b durch einen Winkel $2\phi$ getrennt, der in diesem Beispiel nicht zur gleichmäßigen Kreisteilung passt. Daher gilt hier: $b^4\neq a^4$.

Damit ist ersichtlich, dass $a^n=b^n$ dann gilt, wenn eine der n Wurzeln von $b^n$ auf a fällt – und umgekehrt. Das passiert immer dann, wenn der Winkel $2\phi$ „zwischen a und b“ ein Vielfaches des Winkels $\frac{2\pi}{n}$ ist, denn dies ist der Winkel zwischen zwei benachbarten n-ten Wurzeln. Anders ausgedrückt: Die n-ten Potenzen von a und b sind genau dann gleich, wenn es ein $m\in\mathbb{N}, 0<m<n$ gibt, sodass $2\phi= \frac{2m\pi}{n}$ und folglich $\frac{\phi}{\pi}=\frac{m}{n}$ rational ist:

$$\left(\exists n\in\mathbb{N}:a^n=b^n\right) \Leftrightarrow \left(\frac{\phi}{\pi}\in\mathbb{Q}\right)$$

$\phi=\frac{m\pi}{n}$ nenne ich dann einen rationalen Winkel.2

Zurück zum Kuchen

Wie schmal Du die Kuchenstücke auch machst: Wenn sie alle gleich groß sind, lässt sich aus ihnen immer nur ein rationaler Teil des Kuchens zusammensetzen – jeder rational mögliche sogar. Hast Du allerdings mit Deinen ersten beiden Schnitten schon einen irrationalen Teil des Kuchens ausgeschnitten, kannst Du es nicht mehr schaffen, den ganzen Kuchen in gleich schmale Stücke zu zerlegen.

Ein paar Krümel mehr an Informationen

Anhand der bekannten Parameter p und q ist oft nur schwer zu erkennen, ob φ ein rationaler Winkel ist. Man kann sich einer Lösung dieses Problems jedoch weiter annähern.

$$\begin{aligned} && \phi ={}& \arccos\left(-\frac{p}{2\sqrt{q}}\right) \\ \Leftrightarrow && \cos\phi ={}& -\frac{p}{2\sqrt{q}} \\ \Leftrightarrow && 2\cos\phi ={}& -\frac{p}{\sqrt{q}} \\ && \delta :={}& -\frac{p}{\sqrt{q}} \end{aligned}$$

Nullstelle des Tschebyschow-Polynoms zweiter Art

Das k-te Tschebyschow-Polynom zweiter Art3 ist rekursiv definiert4 als

$$U_k(x) = \begin{cases} 1 & \mathrm{falls\quad} k=0 \\ 2x & \mathrm{falls\quad} k=1 \\ 2xU_{k-1}(x)-U_{k-2}(x) & \mathrm{falls\quad} k\geq 2 \end{cases}$$

Die Nullstellen liegen bei

$$x_j = \cos\left(\frac{j\pi}{k+1}\right),\quad j=1,\ldots,k$$

Damit ist $U_{n-1}\left(\frac{\delta}{2}\right)=0$ genau dann, wenn φ ein rationaler Winkel ist. Sei $V_k$ ein Polynom

$$V_k(t) = \begin{cases} t & \mathrm{falls\quad} k=0 \\ t^2-1 & \mathrm{falls\quad} k=1 \\ t V_{k-1}(t) - V_{k-2}(t) & \mathrm{falls\quad} k\geq 2 \end{cases}$$

Dieses Polynom ist so konstruiert, dass für natürliche n stets $V_n(2x)=U_{n-1}(x)$ gilt. Ist $\frac{\delta}{2}$ eine Nullstelle von $U_{n-1}$, dann ist δ eine Nullstelle von $V_n$ – und umgekehrt.

Aus der rekursiven Definition geht hervor, dass $V_n$ ein normiertes Polynom5 mit ganzzahligen Koeffizienten ist. Ist φ ein rationaler Winkel, ist δ demnach eine ganzalgebraische Zahl. Es gilt für natürliche n:

$$\left(a^n=b^n\right) \Leftrightarrow \left(V_n\left(\delta\right)=0\right)$$
  1. Betrachtet wurden Bildungsgesetze und Grenzwerte zweier Folgenscharen α und β mit den Parametern p und q unter der Bedingung $p^2>4q$, das heißt bei positiver Diskriminante.
  2. Achtung: Der rationale Winkel misst einen rationalen Teil des ganzen Kreises und das Gradmaß des Winkels ist rational. Das Bogenmaß ist irrational.
  3. Dank an Warren D. Smith („Pythagorean triples, rational angles, and space-filling simplices. Chapter 3: The transcendence of certain angles, lemma 3“) fürs Stoßen auf die Tschebyschow-Polynome zweiter Art.
  4. Englische Wikipedia: Chebyshev polynomials, Abrufdatum 2010-03-06
  5. Normiertes – auch monisches – Polynom: Der Koeffizient der höchsten Potenz ist gleich 1.