Der Würfel, ein optimaler Quader

Es gibt gewiss eine Unzahl Wege, um zu zeigen, dass der Würfel das größte Volumen aller Quader im Verhältnis zu seiner Oberfläche besitzt. Dass der Würfel in diesem Sinne also ein „optimaler“ Quader ist.

Ein Ansatz für einen indirekten Beweis sieht so aus: Zuerst zeigt man, dass ein Quadrat bei gleichem Flächeninhalt den kleinsten Umfang aller Rechtecke besitzt. Als zweites nimmt man an, man könne einen „optimalen“ Quader finden, der kein Würfel ist. Man spinnt weiter, welche Schlüsse aus dieser Annahme folgen und gelangt mithilfe der einfacheren Aussage über das Quadrat zu einem Widerspruch.¹ Die Annahme kann dann nicht richtig sein. Wenn es also keinen „optimalen“ Quader gibt, der kein Würfel ist, bleibt nur der Würfel als Kandidat übrig.

Ein anderer Ansatz bedient sich der Differentialrechnung. Im Prinzip nahe liegend, handelt es sich doch um ein Extremwertproblem. Aber auch nur nahe liegend, wenn einem die Differentialrechnung vertraut ist. Zumal nahe liegender Weise eine Ableitung einer Funktion mit mehreren Veränderlichen in Frage kommt, welche im Grundkurs Mathematik nicht einmal im Abitur auf dem Lehrplan steht, vielleicht doch nicht für jeden so nahe liegend.

Ich wollte einen direkten Beweis finden, der nicht mehr als einen Schulabschluss der 10ten Klasse voraussetzt. Lustiger Weise kam ich während meines Studiums der Angewandten Mathematik nicht darauf. War ich zu sehr im aktuellen Stoff gefangen und hatte den Blick für die grundlegenden Lösungswege verloren? Da es genug anderes zu tun gab, legte ich das Problem schnell zur Seite. Nun ist Zeit, den Beweis nachzuholen. :-) Doch zuvor die Frage:

Wozu ist das gut?

Gut ist das für die Energiebilanz eines Hauses, beim Backen eines krustenarmen Kastenbrotes, bei der materialsparenden Verpackung von Produkten sowie beim Bau eines effizienten Raumschiffes. Auch bei der Form des Eises im Erfrischungsgetränk spielt diese Überlegung eine Rolle.

Vorbetrachtungen

Es sollen keine exotischen „Minus-Würfel“ oder „Null-Quader“ betrachtet werden. Alle Kanten haben positive Längen.

Würfel

Für das Volumen $V_W$, die Oberfläche $A_W$ und die Kantenlänge b eines Würfels gelten:

$$\begin{aligned} && V_W &= b^3 \\ && A_W &= 6b^2 \\ \Leftrightarrow && \sqrt{\frac{A_W}{6}} &= b \end{aligned}$$

Das „⇔“ vor der letzten Zeile bedeutet einfach, dass diese und die vorhergehende Zeile – unter den gegebenen Voraussetzungen – äquivalent sind.

Quader

Für das Volumen $V_Q$, die Oberfläche $A_Q$ und die Kantenlängen c, d und e eines Quaders gelten:

$$\begin{aligned} V_Q &= cde \\ A_Q &= 2cd + 2ce + 2de \end{aligned}$$

Wählt man c als Bezeichnung für die kürzeste Kante des Quaders, kann man die anderen $d=c+x$ und $e=c+y$ schreiben.

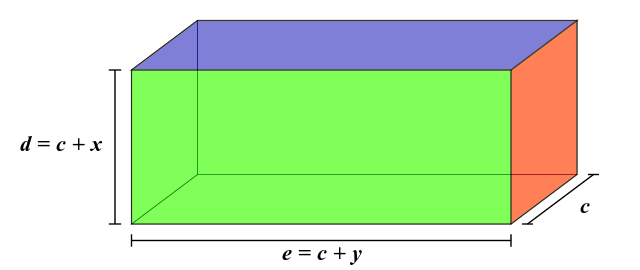
Die Gleichungen für Volumen und Oberfläche sehen dann so aus:

$$\begin{aligned} V_Q &= c(c+x)(c+y) \\ &= c^3+c^2x+c^2y+cxy \\ A_Q &= 2c(c+x)+2c(c+y)+2(c+x)(c+y) \\ &= 6c^2+4cx+4cy+2xy \end{aligned}$$

Wobei $x,y \geq 0$ und auch $c > 0$ zutreffen, denn wie gesagt: Alle Längen sind positiv.

Und los…

Behauptung

Ein Würfel hat mindestens das gleiche Volumen wie ein beliebiger Quader mit derselben Oberfläche. Sind die Volumen gleich, dann muss auch der Quader ein Würfel sein. Als Formel notiert (darf aber ignoriert werden):

$$\left(A_W = A_Q\right) \Leftrightarrow \left(\left(V_W \geq V_Q\right) \wedge \left(\left(V_W=V_Q\right)\Leftrightarrow\left(x=y=0\right)\right)\right)$$

Einfach ausgedrückt: Von allen Quadern hat der Würfel das „optimale“ Verhältnis aus Volumen und Oberfläche.

Beweis

Zuerst baue man sich einen Würfel, der dieselbe Oberfläche wie ein beliebiger Quader hat. Dafür kombiniere man die Gleichungen der Quader-Oberfläche und der Kantenlänge des Würfels. Dann wende man die Volumenberechnung des Würfel an:

$$\begin{aligned} b &= \sqrt{\frac{A_Q}{6}} \\ &= \sqrt{\frac{6c^2+4cx+4cy+2xy}{6}} \\ &= \sqrt{c^2+\frac{2}{3}cx+\frac{2}{3}cy+\frac{1}{3}xy} \\ V_W &= b^3 \\ &= \left(\sqrt{c^2+\frac{2}{3}cx+\frac{2}{3}cy+\frac{1}{3}xy}\right)^3 \end{aligned}$$

Nun zeige man, dass das Volumen dieses Würfels mindestens so groß wie das Volumen des Quaders ist:

$$\begin{aligned} && V_W &\geq V_Q \\ \Leftrightarrow && \left(\sqrt{c^2+\frac{2}{3}cx+\frac{2}{3}cy+\frac{1}{3}xy}\right)^3 &\geq c^3+c^2x+c^2y+cxy \\ \Leftrightarrow && \left(c^2+\frac{2}{3}cx+\frac{2}{3}cy+\frac{1}{3}xy\right)^3 &\geq \left(c^3+c^2x+c^2y+cxy\right)^2 \\ \Leftrightarrow && \left(c^2+\frac{2}{3}cx+\frac{2}{3}cy+\frac{1}{3}xy\right)^3 - \left(c^3+c^2x+c^2y+cxy\right)^2 &\geq 0 \end{aligned}$$

… jetzt die Potenzen auflösen, also „die Klammern ausmultiplizieren“ – zugegeben, da ist etwas Schreibarbeit nötig, aber dem Prinzip nach nicht schwer …

$$\begin{aligned} \Leftrightarrow && \left( c^6 +2 c^5 x +2 c^5 y +\frac{4}{3} c^4 x^2 +\frac{11}{3} c^4 x y +\frac{4}{3} c^4 y^2 +\frac{8}{27} c^3 x^3 +\frac{20}{9} c^3 x^2 y +\frac{20}{9} c^3 x y^2 +\frac{8}{27} c^3 y^3 +\frac{4}{9} c^2 x^3 y +\frac{11}{9} c^2 x^2 y^2 +\frac{4}{9} c^2 x y^3 +\frac{2}{9} c x^3 y^2 +\frac{2}{9} c x^2 y^3 +\frac{1}{27} x^3 y^3 \right) - \left( c^6 +2 c^5 x +2 c^5 y + c^4 x^2 +4 c^4 x y + c^4 y^2 +2 c^3 x^2 y +2 c^3 x y^2 + c^2 x^2 y^2 \right) &\geq 0 \end{aligned}$$

… weiter zusammenfassen kann nicht schaden …

$$\begin{aligned} \Leftrightarrow && \frac{1}{3}\left( c^4 x^2 - c^4 x y + c^4 y^2 +\frac{8}{9} c^3 x^3 +\frac{2}{3} c^3 x^2 y +\frac{2}{3} c^3 x y^2 +\frac{8}{9} c^3 y^3 +\frac{4}{3} c^2 x^3 y +\frac{2}{3} c^2 x^2 y^2 +\frac{4}{3} c^2 x y^3 +\frac{2}{3} c x^3 y^2 +\frac{2}{3} c x^2 y^3 +\frac{1}{9} x^3 y^3 \right) &\geq 0 \\ \Leftrightarrow && c^4\underbrace{\left(x^2-xy+y^2\right)}_{\stackrel{\left(\left(x-y\right)^2+xy\right)}{\textrm{2te binomische Formel}}} +\frac{8}{9} c^3 x^3 +\frac{2}{3} c^3 x^2 y +\frac{2}{3} c^3 x y^2 +\frac{8}{9} c^3 y^3 +\frac{4}{3} c^2 x^3 y +\frac{2}{3} c^2 x^2 y^2 +\frac{4}{3} c^2 x y^3 +\frac{2}{3} c x^3 y^2 +\frac{2}{3} c x^2 y^3 +\frac{1}{9} x^3 y^3 &\geq 0 \end{aligned}$$

Nun ist ersichtlich, dass die Ungleichung stimmt. Alle Summanden auf der linken Seite sind größer oder gleich null. Auch erkennt man, dass nur dann Gleichheit hergestellt werden kann, wenn $x=y=0$, also auch der Quader ein Würfel ist. Der Quader reicht nur dann an den Würfel heran, wenn er selbst zum Würfel wird. Beweis erbracht. :-)

Auch mal probieren?

Wie wäre es zum Beispiel mit einem Beweis, dass der Würfel von allen Quadern das größte Verhältnis aus Volumen und Gesamtkantenlänge besitzt? Oder mit weniger Schreibarbeit: Dass das Quadrat von allen Rechtecken das größte Verhältnis von Flächeninhalt zum Umfang hat? Im Prinzip geht es genauso wie dieser Beweis. Und gewiss auch noch anders.

Etwas ausführlicher: Jeder nicht-würfelförmiger Kandidat für einen „optimalen“ Quader besitzt gegenüberliegende Seitenflächen, die keine Quadrate sind. Schnappt man sich davon eine als Grundfläche, kann man sie und die ihr gegenüberliegende durch Quadrate mit der gleichen Fläche aber geringerem Umfang ersetzen. Das Quader-Volumen bleibt dabei gleich, denn weder Grundfläche noch Höhe wurden geändert, und Volumen ist Grundfläche mal Höhe. Ein geringerer Umfang der Grundfläche bedeutet aber bei gleicher Höhe eine kleinere Mantelfläche, denn Mantelfläche ist Umfang der Grundfläche mal Höhe, und letztendlich eine kleinere Oberfläche des ganzen neuen Quaders. Gleiches Volumen, kleinere Oberfläche: Damit wäre der neue Quader „optimaler“ als der „optimalste“ Quader – das geht freilich nicht. Und dadurch ist die Annahme, ein nicht-würfelförmiger Quader könne das optimale Volumen-Oberfläche-Verhältnis aller Quader aufweisen, widerlegt. Als Kandidat für eine optimale Form bleibt nur der Würfel übrig.